行测备考：均值不等式求极值 -亚博188网站

【考试咨询】全国公考交流群（日更课）：825845872｜微信公众号：展鸿教育｜官老师：18969902976

亚博188网站-亚博游戏app｜｜｜

极值问题是行测数量关系中较为常见的一类问题，其中均值不等式求极值，大家在学生时代接触过，但现在可能感觉既陌生又熟悉，印象已经并不深刻了。今天整理了有关均值不等式求极值的知识点，为大家答疑解惑。

一、概念

若a，b是实数，则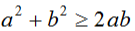，等号当且仅当a=b的时候取得。

二、推论

和定差小积最大，当正实数a、b的和为定值时，当且仅当a=b，a与b的乘积可取到最大值。

三、应用

【例1】某商品的进货单价为80元，销售单价为100元，每天可售出120件。已知销售单价每降低1元，每天可多售出20件。若要实现该商品的销售利润最大化，则销售单价应降低的金额是（    ）。

a.5元     b.6元     c.7元     d.8元

1.【答案】c。解析：设应降低x元，总利润为y元，则降低后的销售单价为（100-x）元，销量为（120 20x）件，进货单价为80元，则总利润y=（100-x-80）×（120 20x），将其化简成函数式为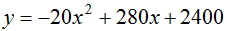，根据一元二次函数图像性质，当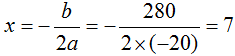时，y最大。故本题选c。

【例2】某类商品按质量分为8个档次，最低档次商品每件可获利8元，每提高一个档次，则每件商品的利润增加2元。最低档次商品每天可产出60件，每提高一个档次，则日减少5件。若只生产其中某一档次的商品，则每天能获得的最大利润是（    ）元。

a.620     b.630     c.640     d.650

2.【答案】c。解析：设提高x档，则每件产品的利润增加2x元，日产量减少5x件，总利润为y元，每天获得的利润为y=（8 2x）×（60-5x）=10×（4 x）×（12-x）元，因为（4 x） （12-x）=16是定值，根据均值不等式原理，故当且仅当4 x=12-x时，即x=4时，（4 x）×（12-x）的值最大，即可获得最大利润，为10×（4 4）×（12-4）=640元。故本题选c。